class: center, middle, inverse, title-slide # 债券价格变动与利率期限结构 ### 吴燕丰 ### 江西财经大学 金融学院 ### 2020/04/04 --- ### 债券价格的变动 【例子】有期限为1年、5年、10年、15年和20年，面值都是￥100元的五种债券，息票率都为5%，年付息2次，当前市场利率为5%，未来市场利率可能为4%、5%、6%。 问：以市场利率5%为基准，未来市场利率升级1%时，债券价格变动规律。 .center[ 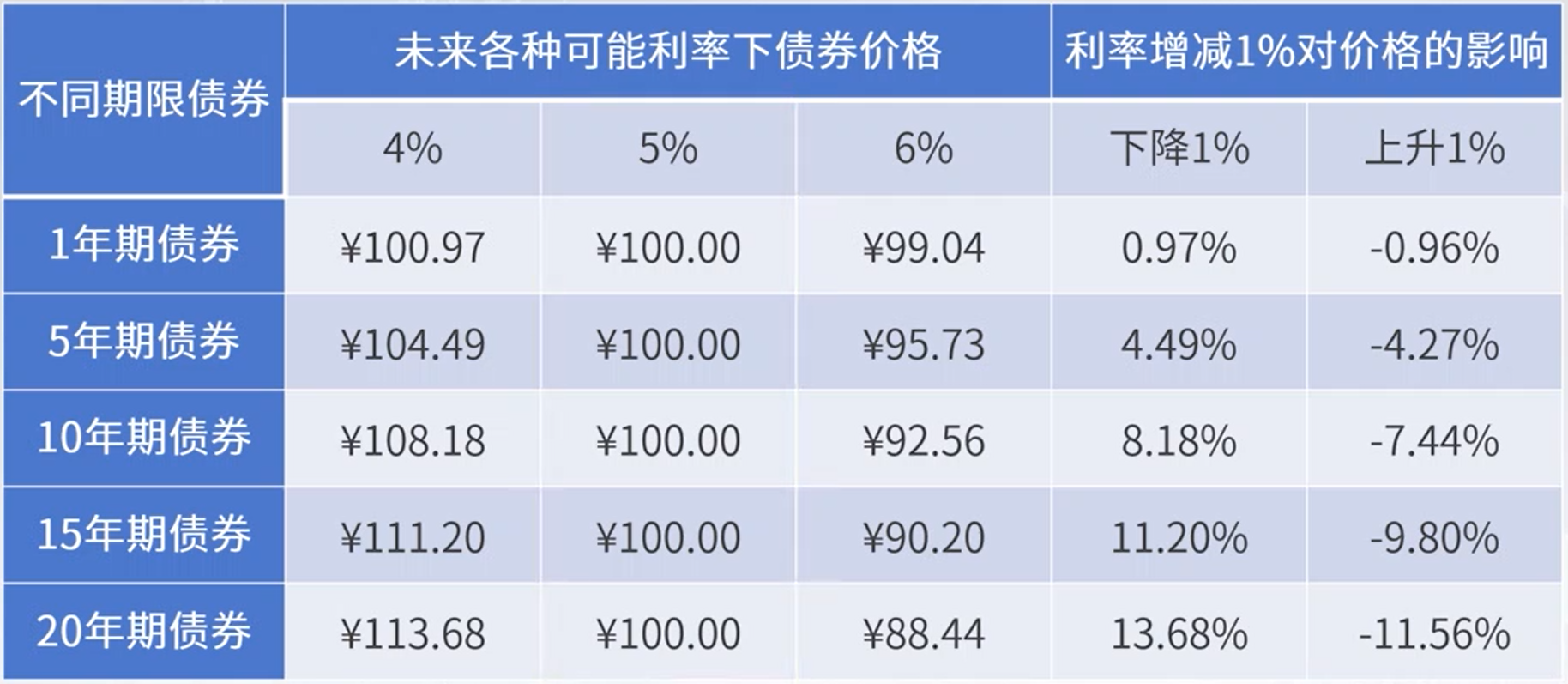 ] --- ### 债券价格公式 债券价格公式： $$ P(y,r,M,T) = \sum_{t=1}^{T}\frac{M\times r}{(1+y)^t} + \frac{M}{(1+y)^T} $$ 债券价格 `\(P\)` 如下量的函数： - 到期收益率 `\(y\)` （市场利率） - 息票率 `\(r\)` - 面值 `\(M\)` - 债券剩余期限 `\(T\)` 债券价格如何随这些量变化？ $$ \frac{dP}{dy} = ?, \quad \frac{dP}{dr} = ?, \quad \frac{dP}{dM} = ?, \quad \frac{P(T+1)-P(T)}{(T+1)-T}=?. $$ --- ### 债券价格变动六大定理 **定理一**：债券价格与市场利率成反比 $$ \frac{dP}{dy} <0. $$ 求导过程为： `\begin{align} P &= \sum_{t=1}^T\frac{M\times r}{(1+y)^t} + \frac{M}{(1+r)^T}, \\ \frac{dP}{dy} &=\sum_{t=1}^{T}\frac{-t\times M\times r}{(1+y)^{t+1}} - \frac{T\times M}{(1+y)^{T+1}}<0. \end{align}` -- .center[  ] --- ### 债券价格变动六大定理 **定理二**：债券价格受利率变动的影响大小，与当期市场利率的高低成反比 `$$|\frac{dP}{dy_1}| > |\frac{dP}{dy_2}| , \text{ 当 } y_1 < y_2; \frac{d^2P}{dy^2}>0.$$` `\begin{align} \frac{dP}{dy}&= \sum_{t=1}^{T}\frac{-t\times M\times r}{(1+y)^{t+1}} - \frac{T\times M}{(1+y)^{T+1}}<0\\ \frac{d^2P}{dy^2}&=\sum_{t=1}^{T}\frac{t\times(t+1)\times M\times r}{(1+y)^{t+2}}+\frac{T\times(T+1)\times M}{(1+y)^{T+2}}>0 \end{align}` .center[  ] --- ### 债券价格变动六大定理 **定理三**：长期债券的价格受市场利率变动的影响大于短期债券 `$$|\frac{dP(T_1)}{dy}| > |\frac{dP(T_2)}{dy}|, \text{ 当 }T_1 > T_2$$` `\begin{align} \frac{dP(T)}{dy}&= \sum_{t=1}^{T}\frac{-t M r}{(1+y)^{t+1}} - \frac{T M}{(1+y)^{T+1}}\\ \frac{dP(T+1)}{dy}&= \sum_{t=1}^{T+1}\frac{-t M r}{(1+y)^{t+1}} - \frac{(T+1) M}{(1+y)^{T+2}}\\ \frac{dP(T+1)}{dy}-\frac{dP(T)}{dy}&= -\frac{(T+1) M r}{(1+y)^{T+2}}-\frac{(T+1) M}{(1+y)^{T+2}}+\frac{T M}{(1+y)^{T+1}}\\ &=\frac{M}{(1+y)^{T+2}}[-(T+1)r-(T+1)+T(1+y)]\\ &=\frac{M}{(1+y)^{T+2}}[-Tr+Ty-r-1]<0 \text{ if } r=y, \end{align}` `\(\text{ 或 } y-r < \frac{r+1}{T}\)` 。 --- ### 定理三（续） .center[  ] --- ### 债券价格变动六大定理 **定理四**：债券价格受市场利率变动影响的程度随到期期限的延长而递减 $$|\frac{dP(T+2t)}{dy}-\frac{dP(T+t)}{dy}| < |\frac{dP(T+t)}{dy}-\frac{dP(T)}{dy}| $$ .center[  ] --- ### 债券价格变动六大定理 **定理五**：债息率越低的债券受市场利率变动的影响越大 `$$|\frac{dP(r_1)/dy}{P(r_1)}| > |\frac{dP(r_2)/dy}{P(r_2)}|, \text{ 当 } r_1<r_2$$` `\begin{align} \frac{dP(r_1)}{dy}-\frac{dP(r_2)}{dy} &= \sum_{t=1}^{T}\frac{-tMr_1+tMr_2}{(1+y)^{t+1}}\\ &=(r_2-r_1)\sum_{t=1}^{T}\frac{tM}{(1+y)^{t+1}}>0\text{ if }r_1<r_2 \end{align}` `\begin{align} |dP(r_1)/dy| &< |dP(r_2)/dy| \\ P(r_1) & < P(r_2) \\ |\frac{dP(r_1)/dy}{P(r_1)}| &> |\frac{dP(r_2)/dy}{P(r_2)}| \end{align}` --- ### 债券价格变动六大定理 **定理六**：市场利率下降使债券价格上涨的幅度，大于市场利率上升使债券价格下降的幅度 `$$\frac{P(y_1)-P(y)}{P} > \frac{P(y)-P(y_2)}{P}, \text{ 当 }y_1<y<y_2$$` 与**定理二**类似。 .center[] --- ### 到期收益率与实际收益率 【例子】假设年付息一次，息票率为8%，面值为1000元的4年期债券，成交价格为990。问： - 持有到期时该债券的到期收益率是多少？ - 如果期间再投资收益率分别为6%、8.3%和10%，则投资该债券实际年收益率依次是多少？ 计算方式： - 到期收益率为如下方程的解， `\(y\approx 8.3\%\)` ， $$ 990\text{ (现值) }=\sum_{t=1}^{4}\frac{1000\times8\%}{(1+y)^t} + \frac{1000}{(1+y)^4} $$ - 再投资收益率为6%时，实际收益率为满足下面方程的r，其他情况类似计算 $$ \left[\sum_{t=1}^{4}1000\times8\%\times(1+6\%)^{4-t} + 1000\right] \text{ (终值) }= 900\times(1+r)^4 $$ --- ### 到期收益率 到期收益率与实际收益率的关系 到期收益率为满足如下方程的解（ `\(y = 8.3%\)` ）： $$ 990\times(1+y)^4 = \sum_{t=1}^{4}1000\times 8\%\times(1+y)^{4-t} + 1000 $$ 再投资率为8.3%对应的实际投资率r，为满足如下方程的解： $$ 990\times(1+r)^4 = \sum_{t=1}^{4}1000\times 8\%\times(1+8.3\%)^{4-t} + 1000 $$ 背后的假设： 1. 投资者持有债券直至到期（持有到期） 2. 发行人按约定支付现金流（不违约） 3. 各期利息收入在债券剩余期限内再投资，且再投资率等于到期收益率。 --- ### 零息债券 P：债券价格（当前价格）；M：债券面值；T：债券剩余期限；y：到期收益率（**即期利率**） $$ P=\frac{M}{(1+y)^T} \implies y = \sqrt[T]{\frac{M}{P}} - 1 $$ 为了突出显示即期利率对剩余期限的依赖，记 y 为 `\(y_T\)` 。 【例子】 $$ 797.19\text{ (现值) } = \frac{1000\text{ (终值) }}{(1+y_2)^2} \implies y_2 = 12\% $$ $$ 751.31\text{ (现值) } = \frac{1000\text{ (终值) }}{(1+y_3)^3}\implies y_3=10\% $$ --- ### 即期利率与远期利率 即期利率：此刻（即期）获得贷款，到期支付本息和，对应的利率。记号： `\(S_T\)` 远期利率：未来（远期）获得贷款，到期支付本息和，对应的利率。记号： `\(f_{t,T}\)` 即期利率 `\(S_T\)` 也可以写成 `\(S_{0,T}\)` 。 远期利率与即期利率的关系 `$$(1+S_T)^T = (1+S_t)\times(1+f_{t,T})^{T-t}$$` 【例子】 `$$(1+S_2)^2 = (1+S_1)\times(1+f_{1,2})^{2-1} \implies f_{1,2} = \frac{(1+S_2)^2}{(1+S_1)} - 1$$` --- ### 即期利率与远期利率（续） 当剩余期限 T>1 年时，有多种组合，即对应不同等价操作。 【例子】T=3年时， `\begin{align} (1+S_3)^3 &= (1+S_1)\times(1+f_{1,3})^2 \\ &= (1+S_1)\times(1+f_{1,2})\times(1+f_{2,3})\\ &= (1+S_2)^2\times(1+f_{2,3}) \end{align}` -- 【例子】T=4年时， `\begin{align} (1+S_4)^4 &= (1+S_1)\times(1+f_{1,4})^3\\ &= (1+S_1)\times(1+f_{1,3})^2\times(1+f_{3,4})\\ &= (1+S_1)\times(1+f_{1,2})\times(1+f{2,4})^2\\ &= (1+S_1)\times(1+f_{1,2})\times(1+f_{2,3})\times(1+f_{3,4})\\ &= \cdots \end{align}` --- ## 利率期限结构理论 利率期限结构（term structure of interest rate）： `\(y(T)\)` ，收益率曲线（yield curve）。 .center[ 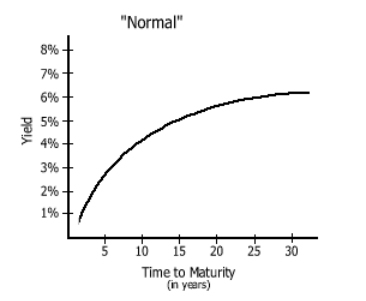 ] .footnote[ [*] 图片来源：[sina blog](http://blog.sina.com.cn/s/blog_47a79fa00101h3ka.html) ] --- ### 收益率曲线的几种类型 .center[ 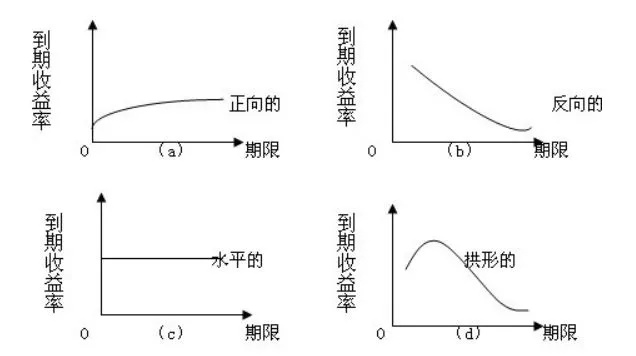 ] .footnote[ [*] 图片来源：[知乎网页](https://zhuanlan.zhihu.com/p/32785022) ] --- ### 对收益率曲线的解释 1. 预期假说： - 市场对未来利率变化的预测是准确的 2. 流动性偏好假说： - 投资人偏好流动性更好的资产（债券），所以倾向短期投资 3. 市场分割理论： - 长期债券市场和短期债券市场是分割的 4. ... --- ### 到期收益率与各期折现率关系 [到期收益率与各期折现率关系](http://www.yyschools.com/bond_price_and_term_structure/bond_price_and_term_structure.html) --- ### End .center[ Questions & Answers ]